B. Ed. Sem IV Maths Method
“ स्वावलंबी शिक्षण हेच आमचे ब्रीद ”
“ स्वावलंबी शिक्षण हेच आमचे ब्रीद ”
– पद्मभूषण डॉ. कममवीर भाऊराव पाटील रयत शिक्षण संस्थेचे आझाद कॉलेज ऑफ एज्युकेिन, सातारा गशणत अध्यापन पद्धती शवभाग बी.एड. शितीय वषम - सत्र चार संपादन प्रा. डॉ. नंदकु मार धनवडे सहयोगी प्राध्यापक आझाद कॉलेज ऑफ एज्यकशन,सातारा ु े 1 �

COURSE 10 – Optional Course
Pedagogy of School Subject at Higher Secondary Level MATHEMATICS Contact Hours: 02 Hours Per Total Marks: 50 week Credit: 02 External Assessment: 35 Total Instructional Hours : 30 Internal Assessment: 15 Unit - I Objectives and strategies of teaching Mathematics (08 hrs, 9 Marks) a) Objectives of teaching Mathematics as prescribed in Higher Secondary Education of Maharashtra state. महाराष्ट्र राज्याने शनधामररत के लेली उच्च माध्यशमक स्तरावरील उद्दिष्ठ्ये b) Procedure, Merits and demerits of Mathematics 2 following strategies of teaching �

Analysis – Synthesis (पथ:करण – संयोजन) ृ Problem Solving (समस्या ननराकरण) Heuristic (स्वयंशोधन) Project (प्रकल्प) Laboratory (प्रयोगशाळा) Brain based learning (में द ू आधाररत अध्ययन) Activity based Learning (कती आधाररत अध्ययन) ृ Computer Assisted Instruction (CAI) (संगणक सहायनयत अंनदेशन) ु Reflective and Logical Thinking (ववमशी ववचार) Open Ended Questions (HOT Questions) (उच्च ववचार प्रश्न) Unit I A) महाराष्ट्र राज्याने शनधामररत के लेली उच्च माध्यशमक स्तरावरील उद्दिष्ठ्ये Objectives To enable the students 1) to acquire knowledge and critical understanding, particularly by way of motivation and visualization of basic concepts, terms, 3 �

principles, symbols and mastering the underlying processes
and skills. 2) to apply the knowledge and skills in Mathematics and related problems from other subjects, by more than one method. 3) to develop positive attitude to think, analyze and articulate logically. 4) to develop interest in Mathematics by participating in various related competitions and self-learning. 5) to acquaint students with different aspects of Mathematics used in real life. 6) to develop an interest in students to study Mathematics as a discipline 7) to develop awareness of the need for national integration, protection of an environment, removal of social barriers, elimination of sex biases and observance of small family norm. 8) to develop reverence and respect towards great mathematicians for their contribution to the field of Mathematics. 9) to develop interest in the subject by participating in related competitions 4 �

उद्दीष्टे
ववद्यार्थयाांना सक्षम करण्यासाठी 1) मलभत संकल्पना, संज्ञा, तत्त्वे, चचन्हे , प्रक्रिया आणण कौशल्ये यांचे प्रेरणा ू ू आणण व्हहज्युअलायझेशनच्या मागााने ज्ञान आणण आकलन संपादन करणे. 2) एकापेक्षा जास्त पद्धतींचे गणणत आणण इतर ववषयांशी संबंचधत समस्यांमध्ये ज्ञान आणण कौशल्ये यांचे उपयोजन करणे. 3) ववचार करणे, ववश्लेषण करणे आणण ताक्रककदृष्ट्या स्पष्टट करणे यासाठी ा सकारात्मक दृष्टटीकोन ववकससत करणे. 4) ववववध संबंचधत स्पधाांमध्ये आणण स्वयं -सशक्षणामध्ये भाग घेऊन गणणताची आवड ननमााण करणे. 5) वास्तववक जीवनात वापरल्या जाणार्या गणणताच्या ववववध पैलंबद्दल ू ववद्यार्थयाांना पररचचत करणे. 6) ववद्यार्थयाांना गणणत ही एक ववद्याशाखा म्हणून अभ्यास करण्यास आवड ननमााण करणे. 7) राष्टरीय एकात्मता, पयाावरणाचे रक्षण, सामाव्जक अडथळे दर करणे, लैंचगक ू पक्षपातीपणाचे उच्चाटन आणण लहान कटुंबाचे ननकष पाळणे याववषयीच्या ु गरजेबाबत जागरूकता ववकससत करणे. 8) गणणताच्या क्षेत्रातील योगदानाबद्दल महान गणणतज्ञांप्रती आदरभाव ववकससत करणे. 5 �

9) संबंचधत स्पधाांमध्ये भाग घेऊन या ववषयामध्ये आवड ननमााण करणे.
Unit – I B. 1) पथक्करण पद्धती (Analytic Method) ृ Analytic हा शब्द Analysis या शब्दावरून तयार झालेला आहे आणण Analysis चा अथा आहे To take a part of to separate the things that are together म्हणजेच एकमेकाजवळ असलेल्या बाबी एकमेकापासन स्वतं त्र ू करणे, दर करणे, वेगळे करणे. पथक्करण म्हणजे एखाद्या बाबींचे त्याच्या छो्या ू ृ छो्या भागामध्ये रूपांतर करणे. एखादी समस्या असल्यास त्या समस्येचे नतच्या साध्या, सोप्या व सरळ अशा घटकामध्ये रूपांतर करणे क्रकंवा त्याच्यामध्ये जे लपलेले आहे त्या संबंधात उत्तर शोधण्याचा प्रयत्न करणे या रूपांतर कलेल्या लहान े भागातील परस्पर संबंध शोधणे , तुलना करणे, त्या संबंधी माहीत नसलेल्या बाबींची माहहती समळववणे हे पथक्करणमध्ये अपेक्षक्षत आहे . गणणतात कोणतीही समस्या ृ सोडववण्या अगोदर नतचे पथक्करण कले जाते. कारण गणणतातील कोणत्याही े ृ उदाहरणात काही गोष्टटी हदलेल्या असतात व काही गोष्टटी शोधून काढावयाच्या असतात म्हणन पथक्करण करणे आवश्यक असते. म्हणनच भसमतीतील प्रमेयाची ू ू ू ृ ससद्धता दे ण्यासाठी प्रामुख्याने पथक्करण पद्धती वापरली जाते. गणणत आशयाचे ृ आकलन तकसंगत, ससंगत व मानसशास्त्रीय दृव्ष्टटकोनातून होण्यासाठी पथक्करण ा ु ृ पद्धतीचा स्वीकार अध्यापनासाठी आपण करतो. 'अज्ञाताकडू न ज्ञाताकडे' आणण 6 �

'साध्यापासन पक्षाकडे' (हदलेल्या बाबीकडे) जाणारी पद्धती म्हणजे 'पथक्करण
ू ृ पद्धती' होय. पथक्करण कल्यामुळे बारकावे लक्षात येतात व समस्या सोडववण्यास मदत होते. े ृ पथक्करणात सरुवात ननष्टकषा क्रकंवा अनुमानापासून होते आणण पररकल्पना शेवटी ु ृ माडली जाते तत्व: अज्ञाताकडून ज्ञाताकडे म्हणजेच unknown to known या तत्त्वावर आधाररत ही पद्धती आहे . माहीत नसलेल्या भागाकडून माहीत असलेल्या भागाकडे जाणे ननष्टकषा क्रकंवा अनुमानापासून सुरुवात करून क्रकंवा जे ससद्ध करावयाचे आहे तेथून सरुवात करून पथक्करण करत करत माहीत नसलेल्या भागास माहीत ु ृ असलेल्या भागाशी जोडणे हे पथक्करणात अपेक्षक्षत आहे ृ पथक्करण पद्धतीचे स्वरूप व त्यातील टप्पे (Steps ) पुढीलप्रमाणे ृ स्वरूप / टप्पे (Steps) : हदलेल्या उदाहरणातील राशीचे पथक्करण करणे, ृ पथक्करणातून हदलेल्या बाबींची नोंद करणे. ृ 'काय काढावयाचे' म्हणजे 'साध्य शोधणे' साध्यापासून सुरुवात करून प्रश्न ववचारीत का? या प्रश्नाचे उत्तर शोधीत हदलेल्या बाबी म्हणजे पक्षापयांत पोहोचणे . अशाप्रकारे 'साध्यापासून सुरुवात करून ज्या बाबी हदलेल्या आहे त (पक्ष) तेथपयांत तकसंगत ववचारसरणीचा उपयोग करीत जाणे या पद्धतीला पथक्करण ा ृ पद्धती असे म्हणतात. म्हणजेच ववद्यार्थयाांसमोर एखादे उदाहरण क्रकंवा समस्या ठे वावी त्या उदाहरणात कोणकोणत्या बाबी हदलेल्या आहे त. कोणत्या बाबी शोधायच्या आहे त , ते शोधण्यासाठी कसे प्रयत्न करता येतील, कोणत्या मागााने जाता येईल इत्यादी भाग 7 �

सोप्या प्रश्नातूनववद्यार्थयाांना ववचारून त्या उदाहरणाचे क्रकंवा समस्येचे पथक्करण
ृ करावे लागते. असे पथक्करण करत करत माहीत नसलेल्या भागाशी माहीत ृ असलेल्या भागाचा संबंध जोडत जोडत उत्तरापयांत पोहोचायचे असते. या संपूणा प्रक्रियेत पथक्करणाबरोबर संयोजनाचाही भाग समाववष्टट होत असतो हे ही लक्षात ृ असू द्यावे. पथक्करण पद्धतीचे स्वरूप पुढील पायर्यावरून अचधक स्पष्टट होईल. ृ पथक्करण पद्धतीच्या पायऱ्या पुढील प्रमाणे आहे त. ृ पायरी 1) ज्या राशी काढावयाच्या आहे त त्या ननव्श्चत करणे. पायरी 2) साध्यापासून सरुवात ु करून ते कसे साध्य करायचे? साध्याप्रत जाण्यासाठी कोणकोणत्या गणधमाांचा उपयोग करता येईल असा ववचार करीत ु प्रत्येक प्रश्नानंतर मनात ननमााण होणार्या 'का' या प्रश्नाचे उत्तर शोधीत जाणे. पायरी 3) प्रश्न मासलकच्या रूपाने हदलेल्या राशीपयांत येणे. े या पायऱ्यानुसार उदाहरणे कशी सोडववतात त्याचा ववचार करू. उदा. 1) वतुाळाबाहे रील बबंदतून वतुाळास काढलेल्या स्पसशाका समान लांबीच्या ु असतात आणण स्पसशाका आणण वतूाळमध्य व हदलेला बबंद ू यांना जोडणान्या रे षेमळे ु त्या बबंदच्या हठकाणी होणारे कोन समान मापाचे असतात. ू पायरी 1) (1) शोधून काढावयाच्या बाबी कोणत्या ? (साध्य)(i) l (PT1) = (PT2) (ii) m
(3) वतुाळमध्य C आणण बबंद ू P यांना जोडणारी रे षाखंड PC आहे . P. या
बबंदपाशी स्पसशाकामुळे 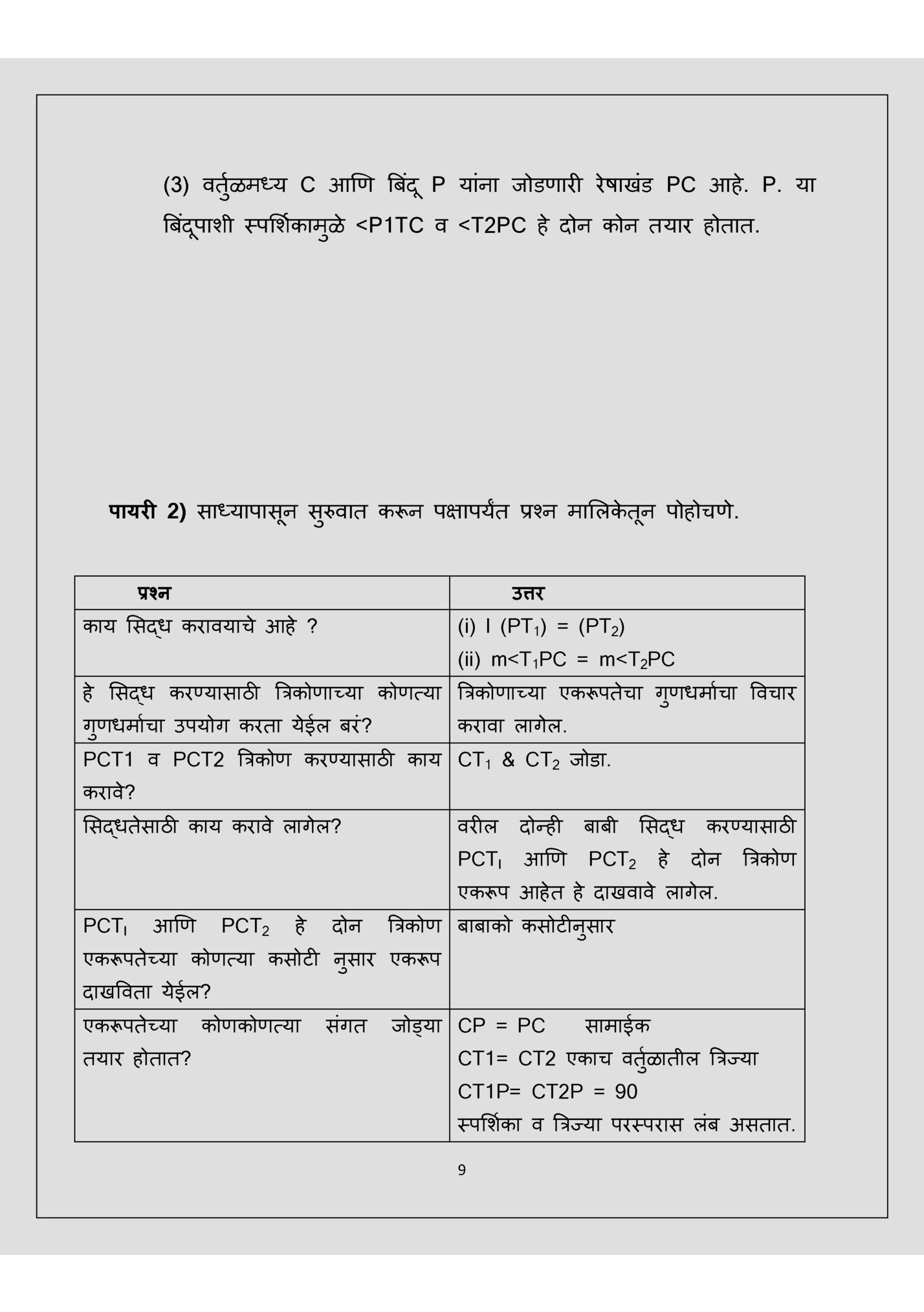
Flipbook Gallery
Magazines Gallery
Catalogs Gallery
Reports Gallery
Flyers Gallery
Portfolios Gallery
Art Gallery
Home
Fleepit Digital © 2021








