VOL.1 S T U D I O S DESIGN & ANALYSIS OF ALGORITHMS BTECH 3RD YEAR UNIT 1 TO UNIT 5 35 PAGES

Unit - 1 DAA/Unit-1 predicting the behaviour of algorithms and selecting the best match for the intended purpose because it helps to understand how an algorithm will perform in different situations. Algorithm Algorithm is a step-by-step procedure, which defines a set of instructions to be executed in a certain order to get the desired output. Characteristics of an algorithm 1. Input: There must be a finite Efficiency of an algorithm can be analysed at two different stages, before implementation and after implementation. They are the following Apriori analysis means, analysis is performed prior to running it on a specific system. This analysis is a stage where a function is defined using some number of inputs for the algorithm. theoretical model. 2. Output: There must be some output Posteriori analysis of an algorithm produced as a result of execution of the means we perform analysis of an algorithm. algorithm only after running it on a 3. Definiteness: Each instruction is clear and unambiguous. 4. Effectiveness: Every step of the algorithm should be basic and essential. 5. Finiteness: The transformation of input to output must be achieved in system. In this analysis, actual statistics like running time and space required, are collected. Types of Analysis The efficiency of some algorithms may vary for inputs of the same size. finite steps, i.e. the algorithm must For such algorithms, we need to stop, eventually! differentiate between the worst case, Analysis of Algorithms Algorithm analysis is the process of evaluating the performance of an average case and best case efficiencies. Best Case Analysis algorithm, usually in terms of its time If an algorithm takes the least amount and space complexity. Algorithm of time to execute a specific set of analysis is an essential tool for input, then it is called the best case 1

time complexity. The best case efficiency of an algorithm is the efficiency for the best case input of size n. Because of this input, the algorithm runs the fastest among all the possible inputs of the same size. Average Case Analysis DAA/Unit-1 1. Space Complexity Space complexity is a measure of the amount of computer memory that an algorithm or a program uses to solve a specific problem as a function of the input size. It quantifies the resources required If the time complexity of an algorithm by an algorithm in terms of the for certain sets of inputs are on an memory space it consumes. average, then such a time complexity When analyzing space complexity, you is called average case time need to consider the memory complexity. required for variables, data Average case analysis provides necessary information about an algorithm’s behavior on a typical or random input. You must make some assumption about the possible inputs of size n to analyze the average case efficiency of algorithm. structures, recursion, and any auxiliary space used by the algorithm. 2.Time Complexity Time complexity is a measure of the amount of time an algorithm takes to complete as a function of the size of the input I.e. amount of time it takes to Worst Case Analysis run an algorithm If an algorithm takes maximum It quantifies the efficiency of an amount of time to execute for a algorithm in terms of the number of specific set of input, then it is called the basic operations it performs with worst case time complexity. The respect to the input size. worst case efficiency of an algorithm is the efficiency for the worst case input of size n. The algorithm runs the longest among all the possible inputs of the similar size because of this input of size n. Performance Issues The total time taken for the execution of the program is the sum of the compilation time and the execution time. (i) Compile time – The time taken for the compilation of the program to 2

DAA/Unit-1 produce the intermediate object code or • The execution time serves as an the compiler version of the program. upper bound on the algorithm’s time (ii) Run time or Execution time - The complexity. time taken for the execution of the • It is defined as the condition that program. The optimized code will take allows an algorithm to complete less time to get executed. statement execution in the longest Time complexity T(P) = c + Tp c -- Compile time Tp -- Run time or execution time amount of time possible. • If f(n) describes the running time of an algorithm, f(n) is O(g(n)) if there exist a positive constant C and n0 such that, Asymptotic Notations 0 ≤ f(n) ≤ c*g(n) for all n ≥ n0 it gives the worst-case complexity of an algorithm. The efficiency of each algorithm can Representation of Big-O Notation be checked by computing its time complexity. The asymptotic notations help to represent the time complexity in a shorthand way. The notations such as O (Big-O), Ώ (Omega), and θ (Theta) are called asymptotic notations. These are the mathematical notations that are used in three different cases of Omega Notation (Ω-Notation): time complexity. • The execution time serves as a Big-O Notation (O-notation): • It returns the highest possible output value (big-O)for a given input. lower bound on the algorithm’s time complexity. • It provides the best case complexity of an algorithm. 3

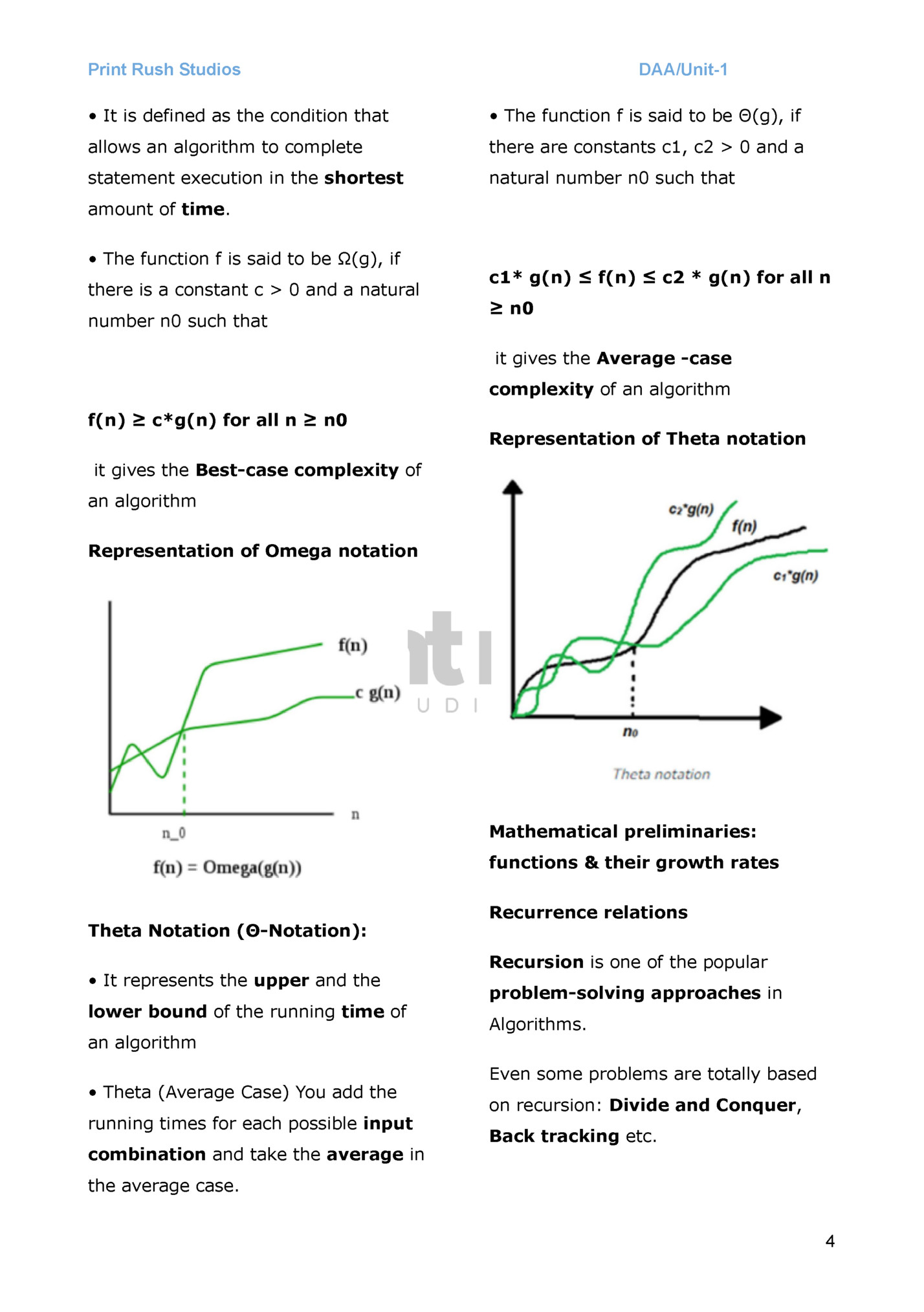
DAA/Unit-1 • It is defined as the condition that • The function f is said to be Θ(g), if allows an algorithm to complete there are constants c1, c2 > 0 and a statement execution in the shortest natural number n0 such that amount of time. • The function f is said to be Ω(g), if there is a constant c > 0 and a natural number n0 such that c1* g(n) ≤ f(n) ≤ c2 * g(n) for all n ≥ n0 it gives the Average -case complexity of an algorithm f(n) ≥ c*g(n) for all n ≥ n0 Representation of Theta notation it gives the Best-case complexity of an algorithm Representation of Omega notation Mathematical preliminaries: functions & their growth rates Theta Notation (Θ-Notation): • It represents the upper and the lower bound of the running time of an algorithm • Theta (Average Case) You add the running times for each possible input combination and take the average in Recurrence relations Recursion is one of the popular problem-solving approaches in Algorithms. Even some problems are totally based on recursion: Divide and Conquer, Back tracking etc. the average case. 4
A recurrence relation is a mathematical equation where any term is defined using its previous terms. We use recurrence relations to analyze the time complexity of recursive algorithms in terms of input size. In recursion, we solve a problem by breaking it down into smaller sub-problems. If the time complexity function of input size n is T(n), then the time complexity of the smaller subproblems will be defined by the same function but in terms of the subproblem's input size. So here is an approach to write T(n) if DAA/Unit-1 1. Substitution Method The substitution method comprises 3 steps 1. Guess the form of the solution 2. Verify by Induction 3. Solve for constants. We substitute the guessed solution for the function when applying the inductive hypothesis to smaller values. Hence the name “Substitution Method.” Our guessed solution must provide an upper bound on the algorithm’s time complexity. If the algorithm’s time complexity is n, we must come up with a guessed solution that is O(n) or greater, such as O(n*logn) or O(n2), which is an upper bound of O(n). Example: we have k number of subproblems: (1) T(n) = T(n/2) + n Also, we have T(1) = 1 Ans- T(n) = T(Input size of 1st subproblem) 1st Try + T(Input size of 2nd subproblem) + Step 1: Guess the form of the solution ….. + T(Input size of kth subproblem) + T(n) = T(n/2) + n Time complexity of additional operations other than recursive calls. Let’s suppose the time complexity of this problem is O(log n), for n ≥ 2. Methods for calculating Time For n = 1, T(1) = 0, which is not the case. Complexity of Recurrence relation Step 2: Verify the induction 1. Substitution Method / Iterative We need to prove that T(n) = c*log n (c is constant) method Equation (1) is T(n) = T(n/2) + n 2. Master’s Method 2.1 Extended Master’s Method 3. Recursive Tree Method ….(1) => T(n) <= c*log(n/2) + n => T(n) <= c*log(n) – c*log 2 + n [Remove c*log 2 as this is a constant] => T(n) <= c*log(n) + n => T(n) = O(n) 5

DAA/Unit-1 So, Induction failed. O(log n) is not an upper bound of O(n). 2nd Try Step 1: Guess the form of the solution T(n) = T(n/2) + n the compiling time, it is 4T(n/2). 4 is very greater than 2 so the result will be not lesser than O(n2). I am sure that the answer will be in n2 form. => T(n) guessed) = O(n2) (we ….(1) Let’s suppose the time complexity of this problem is O(n). I think this will be the upper bound of the given algorithm. Step 2: Verify the induction We need to prove that T(n) = c*n (c is constant) Step 2: Verify the induction We need to prove that T(n) = c*n2 (c is constant) Equation (1) is T(n) = 4T(n/2) + n Equation (1) is T(n) = T(n/2) + n => T(n) <= 4c*(n/2)2 + n => T(n) <= c*n/2 + n => T(n) <= c*n2 + n => T(n) <= c1*n => T(n) <= c*n2 => T(n) = O(n) Here, n2 will be always positive. So, what I assumed was true. Induction Verified. Step 3: Solve for constants c*n/2 + n => 0 Step 3: Solve for constants c* n2 + n => 0 if n => 1 if n => 1 and c => 1, then there is no negative term Then, finally T(n) is O(n). This solution is the upper-bound of the time complexity of the given algorithm. Example: (1) T(n) = 4T(n/2) + n Also, we have T(1) = 1 Ans- and c => 1, then there is no negative term Then, finally T(n) is O(n2). This solution is the upper-bound of the time complexity of the given algorithm. 2. Master’s Method [End Sem 2018 -2M] Step 1: Guess the form of the solution T(n) = 4T(n/2) + n ….(1) Experienced Thinking – If the variable form (n) is divided by 2 then most of the time log n comes in the result. Also, the running time, f(n) is n, so my sixth sense says that the result will not be lesser than (n log n), but in The master theorem is a simplistic way to find time complexity. It works only for the recurrence T(n) = 6

DAA/Unit-1 aT(n/b) + c1*nk, where c1 and k are -> c1*nk is 1 constants. -> Case A occurs The Master Method requires -> (A) if n^(logba) > c1*nk , then memorization of the following 3 cases: answer is O(n^(logba)). Let’s say T(n) = aT(n/b) + c1*nk a ≥ 1, b ≥ 1, c1 ≥ 0 and k are -> O(n) is the answer. 2.1 Extended Master’s method constants (A) if n^(logba) > c1*nk , then This theorem is the extended part answer is O(n^(logba)). of the master’s theorem. If running (B) if n^(logba) < c1*nk , then time in a recurrence equation has a answer is Ω(c1*nk) part of log n, then, by this theorem, we (C) if n^(logba) = c1*nk , then can solve the problem. answer is Ɵ(n^(logba)*logn). T(n) = aT(n/b) + nk*logpn, Q- Find the time complexity of T(n) where a ≥ 1, b ≥ 1, k ≥ 0, p is any real = T(n/2) + n. number. Ans – Apply master’s theorem. (1) If a > bk, then T(n) = θ(nlogba) In this equation, a = 1, b = 2, c1 = 1 (2) If a = bk, and k = 1 -> (a) If p > -1, then T(n) = -> n^(logba) = n^(log21) = n0 = 1 θ(nklogp+1n). -> c1*nk is n -> (b) If p = -1, then T(n) = -> Case B occurs -> (B) if n^(logba) < c1*nk , then answer is Ω(c1*nk) -> Ω(n) is the answer. θ(nkloglogn). -> (c) If p < -1, then T(n) = θ(nk). (3) If a < bk, -> (a) If p ≥ 0, then T(n) = θ(nklogpn). -> (b) If p < 0, then T(n) = O(nk). Q- Find the time complexity of T(n) = 2T(n/2) + 1. Ans – Apply master’s theorem. In this equation, a = 2, b = 2, c1 = 1 Q– Find the time complexity of T(n) = T(n/2) + log n. Ans- Apply Extended master’s theorem. and k = 0 -> n^(logba) = n^(log22) = n1 = n 7

DAA/Unit-1 In this equation, a = 1, b = 2, k = 0 The recurrence tree method is a and p = 1 mathematical Now, Case 2 applies because a = bk analyze the technique time used to complexity of recursive algorithms. It is commonly -> a = 1, bk = 20 = 1 employed when solving recurrence Value of p is 1, means it should be in relations the case of p > -1. divide-and-conquer algorithms. -> T(n) = θ(nklogp+1n). The main steps of the recurrence -> T(n) = θ(n0log1+1n). tree method are -> T(n) = θ(log2n). that arise in 1. Identify the recurrence relation for the algorithm. Q – Find the time complexity of 2. Draw the recurrence tree, showing recursive calls and T(n) = 2T(n/2) + n/log n. their sizes. Ans- 3. Calculate the work done at Apply Extended master’s theorem. each level of the tree. In this equation, a = 2, b = 2, k = 1 4. Sum up the work done and p = -1 across all levels to obtain Now, Case 2 applies because a = bk the time complexity. The height of the recurrence tree -> a = 2, bk = 21 = 2 corresponds to the number of times the Value of p is -1, means it should be in problem the case of p > -1. subproblems until reaching the base -> T(n) = θ(nkloglogn). case. It is typically represented as log -> T(n) = θ(n1loglogn). base b of n, where b is the factor by -> T(n) = θ(n*log2n) θ(n*logn*logn). = is divided into smaller which the problem size reduces at each recursive call. If the equation is T(n) = a T(n/b) + C, where a and b are constants, and C 3. Recursive Tree method is c1*nk, where c1 and k are constants, then we make a recurrence tree. In the recurrence tree method, we make a tree with the help of the [End Sem 2018 -6M] - recurrence equation. Solve Recurrence Relation. 8

Fleepit Digital © 2021