I poliedri regolari sono il punto d'arrivo degli Elementi di Euclide e trovano la loro continuazione nei poliedri tronchi di Archimede. In questo laboratorio di matematica ricreativa rappresentano invece il punto di partenza per introdurre lo studio della geometria solida in 3° media. Ecco 5 solidi particolari. Volete imparare a costruirli con il cartoncino? tetraedro esaedro o cubo ottaedro dodecaedro icosaedro Le fasi della costruzione del cubo Ciascuna fase richiede e sviluppa abilità specifiche: tagliare, piegare, incollare, risolvere problemi tecnici, essere precisi e avere una certa dose di pazienza. Si percepiranno con il tatto gli elementi principali dei poliedri: facce, spigoli, vertici. 1. Ritagliare 2. Piegare 3. Incollare 4. Perfezionare i particolari

I cinque poliedri platonici in cartoncino Il linguaggio dei poliedri Ora è necessario indagare sulle proprietà dei solidi che abbiamo costruito imparando le parole adatte a descrivere gli oggetti e le loro proprietà. Definizione di poliedro Un poliedro è un solido delimitato da un numero finito di poligoni piani, detti facce del poliedro. Definizioni di spigolo e vertice In un poliedro ogni lato di ciascun poligono che costituisce una faccia coincide con il lato di un'altra faccia e viene detto spigolo del poliedro. Ogni vertice di una faccia è vertice di altre facce (almeno 3) e si dice vertice del poliedro. Si dicono facce adiacenti del poliedro due facce che hanno uno spigolo comune. Due facce adiacenti formano un angolo che si chiama diedro. Definizioni di poliedro convesso e poliedro concavo In parole approssimative, un poliedro è concavo se ha delle rientranze, è convesso se non ne ha. Se vogliamo essere più "matematici", possiamo dire: Un poliedro è convesso se ha le seguenti proprietà: • • ogni spigolo è comune esattamente a due facce il piano di ciascuna faccia lascia tutte le rimanenti facce in uno dei due semispazi che individua. Altrimenti è concavo.

Consideriamo un vertice V di un poliedro e gli spigoli in esso incidenti; in genere questi spigoli hanno lunghezze diverse e serve denotare con m la minima di esse; prendiamo su ogni spigolo un punto che disti da V una lunghezza uguale a m. Collegando questi punti otteniamo il "poligono associato al vertice": se questo poligono è regolare si dice che V è un vertice regolare. Ad esempio, nella figura qui sopra, V è un vertice regolare perché, presi VA = VB = VC, si ha che ABC è un poligono regolare (triangolo equilatero) Definizione di poliedro regolare Si dice poliedro regolare un poliedro le cui facce sono tutte poligoni regolari e uguali e i cui vertici sono tutti dotati di poligoni associati uguali e regolari, non necessariamente convessi. Esistono 5 poliedri regolari convessi e 4 poliedri regolari concavi. I solidi platonici I solidi platonici, sono poliedri convessi le cui facce sono poligoni convessi, regolari e uguali. Esistono esattamente 5 poliedri di questo tipo: il tetraedro, il cubo, l'ottaedro, il dodecaedro e l'icosaedro. Le costruzioni dei cinque poliedri regolari sono dimostrate nel libro 13° e ultimo degli Elementi di Euclide. Le proprietà principali dei solidi platonici I solidi platonici hanno le seguenti proprietà: • • • • le facce sono tutte poligoni regolari uguali; i vertici giacciono tutti su una sfera; gli angoli diedri sono tutti uguali; tutti i vertici sono circondati dallo stesso numero di facce. Contiamo le facce, gli spigoli e i vertici Solido facce (F) spigoli (S) vertici (V) tetraedro 4 6 4 cubo 6 12 8 ottaedro 8 12 6 dodecaedro 12 30 20 icosaedro 20 30 12 La formula di Eulero Osservando i dati della tabella, si ricava facilmente la seguente relazione: V=S-F+2 che è detta formula di Eulero, dal nome Leonard Euler, il grande matematico svizzero del 1700. Più in generale, la formula di Eulero afferma che per l'intera classe dei poliedri convessi, ma anche per la più vasta gamma dei poliedri a superficie semplicemente connessa (detto banalmente, quei poliedri che non presentano "buchi" o "manici"), vale l'uguaglianza: F-S+V=2

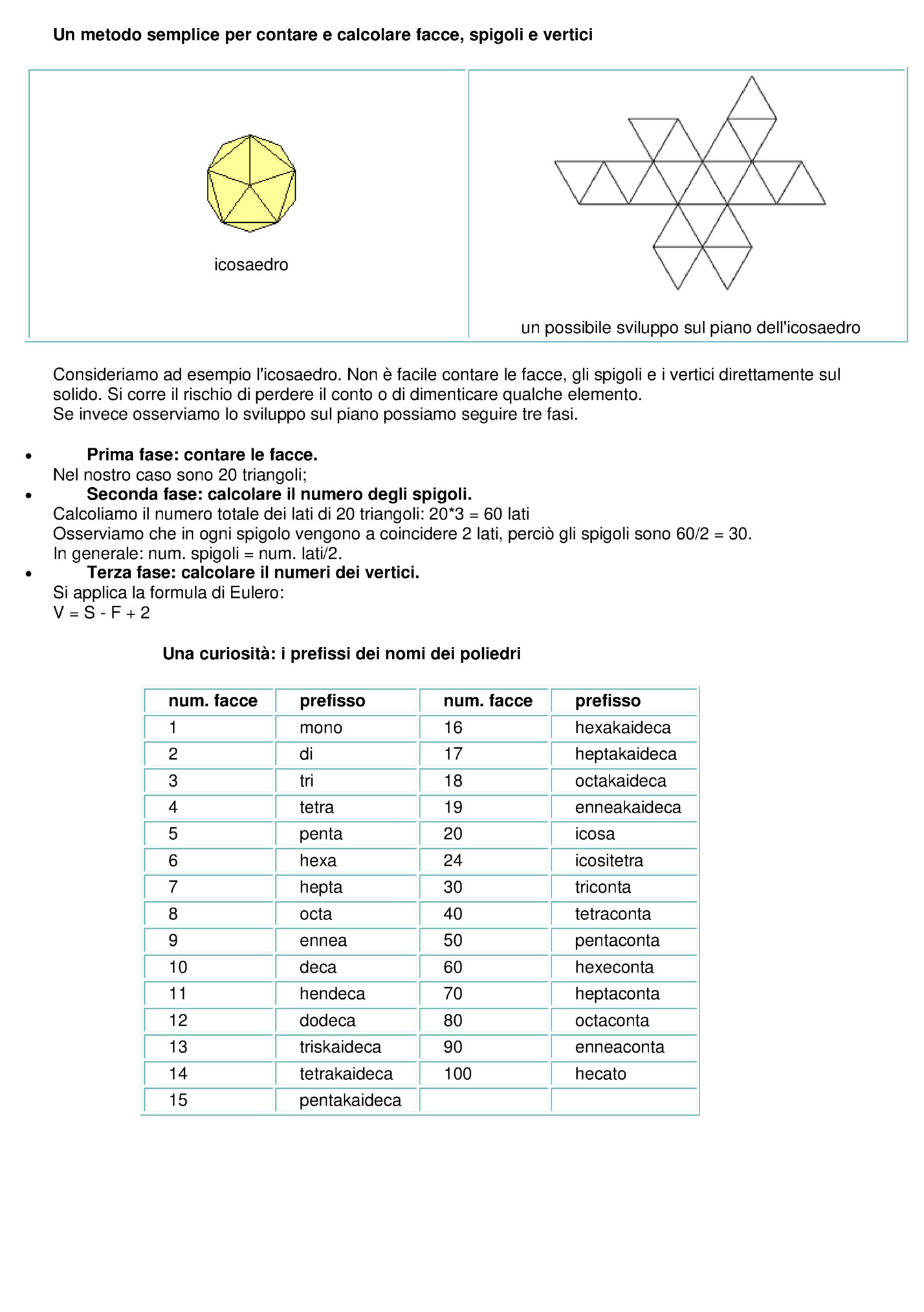
icosaedro un possibile sviluppo sul piano dell'icosaedro Consideriamo ad esempio l'icosaedro. Non è facile contare le facce, gli spigoli e i vertici direttamente sul solido. Si corre il rischio di perdere il conto o di dimenticare qualche elemento. Se invece osserviamo lo sviluppo sul piano possiamo seguire tre fasi. • • • Prima fase: contare le facce. Nel nostro caso sono 20 triangoli; Seconda fase: calcolare il numero degli spigoli. Calcoliamo il numero totale dei lati di 20 triangoli: 20*3 = 60 lati Osserviamo che in ogni spigolo vengono a coincidere 2 lati, perciò gli spigoli sono 60/2 = 30. In generale: num. spigoli = num. lati/2. Terza fase: calcolare il numeri dei vertici. Si applica la formula di Eulero: V=S-F+2 Una curiosità: i prefissi dei nomi dei poliedri num. facce prefisso num. facce prefisso 1 mono 16 hexakaideca 2 di 17 heptakaideca 3 tri 18 octakaideca 4 tetra 19 enneakaideca 5 penta 20 icosa 6 hexa 24 icositetra 7 hepta 30 triconta 8 octa 40 tetraconta 9 ennea 50 pentaconta 10 deca 60 hexeconta 11 hendeca 70 heptaconta 12 dodeca 80 octaconta 13 triskaideca 90 enneaconta 14 tetrakaideca 100 hecato 15 pentakaideca
Il filosofo greco Platone utilizzò i 5 poliedri regolari convessi nel suo libro intitolato Timeo, del 350 a.C., per spiegare il mondo naturale. Per questo essi sono anche chiamati figure cosmiche. Platone associò quattro poliedri a quelli che al suo tempo erano ritenuti i quattro elementi fondamentali della natura, acqua, aria, terra, fuoco: • • • • l'icosaedro all'acqua; l'ottaedro all'aria; il cubo alla terra; il tetraedro al fuoco. Il suo solido preferito era il dodecaedro del qual scrisse: “Restava una quinta combinazione e il Demiurgo (Dio) se ne giovò per decorare l’universo.” La scoperta di questa figura risale almeno al VI sec. a. C., poiché oggetti a forma di dodecaedro appartenenti a quel periodo, sono stati rinvenuti in vari siti archeologici; i cristalli di pirite, che hanno forma dodecaedrica quasi perfetta, che si potevano rinvenire facilmente in molte zone della Magna Grecia, possono essere stati la fonte di ispirazione. Cristalli di pirite (ferro) in forma cubica Cristalli di pirite (ferro) in forma dodecaedrica Solido platonico Solido platonico è sinonimo di solido regolare e di poliedro convesso regolare e si definisce come poliedro convesso che ha per facce poligoni regolari congruenti (cioè sovrapponibili esattamente) e che ha tutti gli spigoli e i vertici equivalenti. Ne consegue che anche i suoi angoloidi hanno la stessa ampiezza. I cinque poliedri convessi regolari ( solidi Platonici ) tetraedro esaedro o cubo ottaedro dodecaedro icosaedro (Animazione) (Animazione) (Animazione) (Animazione) (Animazione) Il nome di ogni figura è derivata dal numero delle sue facce, rispettivamente 4, 6, 8, 12, e 20

Soltanto il triangolo equilatero, il quadrato e il pentagono regolare possono essere facce di poliedri regolari; infatti in un vertice di un poliedro devono convergere almeno 3 facce che non stiano sullo stesso piano; quindi la somma dei loro angoli deve essere inferiore a 360° . Ogni angolo di un triangolo equilatero misura 60° : è quindi possibile far incontrare in un vertice 3 facce (3 x 60 = 180) ottenendo un tetraedro regolare, 4 facce (4 x 60 = 240) ottenendo un ottaedro regolare e 5 facce (5 x 60 = 300) ottenendo un icosaedro regolare. Ogni angolo di un quadrato misura 90° è quindi possibile far incontrare in u n vertice 3 facce (3 x 90 = 270) : ottenendo un cubo. Ogni angolo di un pentagono regolare misura 108° è quindi possibile far incon trare in un vertice 3 facce (3 x . 108 = 324) ottenendo un dodecaedro regolare. Ogni angolo di un esagono regolare misura 120° e quindi 3 facce che si incontrassero in un vertice risulterebbero sullo stesso piano (3 x 120 = 360).

È possibile dimostrare che non esistono più di cinque poliedri regolari anche a partire dalla Relazione di Eulero. Sia dato poliedro con F facce, ognuna delle quali è un poligono regolare con n lati e nel quale, ad ogni vertice, si incontrano r spigoli, i quali sono in totale S. La totalità degli spigoli moltiplicata per due equivale al numero delle facce moltiplicate per il numero n di lati, perché moltiplicando il numero di facce per il numero di lati di ogni faccia ogni spigolo è contato due volte. nF = 2S Inoltre, la totalità degli spigoli moltiplicata per due equivale al numero dei vertici V moltiplicati per il numero r di spigoli che si incontrano in essi, perché ogni spigolo collega due vertici. rV = 2S Quindi si ottiene e sostituendo questi valori nella caratteristica di Eulero-Poincaré V+F−S=2 e, dividendo per 2S, si arriva a n ed r devono essere maggiori o uguali a tre, poiché un poligono deve avere almeno tre lati ed almeno tre lati devono incontrarsi nel vertice di ciascuno degli angoloidi di un poliedro. n ed r non possono essere, inoltre, pari entrambi a quattro poiché in tal caso il primo membro dell'equazione sarebbe uguale a 0, mentre 1/S è positivo. Se n ed r fossero poi contemporaneamente maggiori di quattro, S dovrebbe essere negativo; questa possibilità è quindi esclusa, ed almeno uno deve essere tre. Se n=3, si ha e quindi r può essere uguale solo a 3, 4 o 5, casi che corrispondono rispettivamente al tetraedro, all'ottaedro e all'icosaedro. Allo stesso modo, se r=3 n può assumere solo i valori 3, 4 o 5. 3 può essere scartato perché lo abbiamo considerato nel caso precedente; restano i casi 4 e 5, che corrispondono al cubo e al dodecaedro. Non esistono altri casi possibili, e quindi esistono al più cinque poliedri regolari.

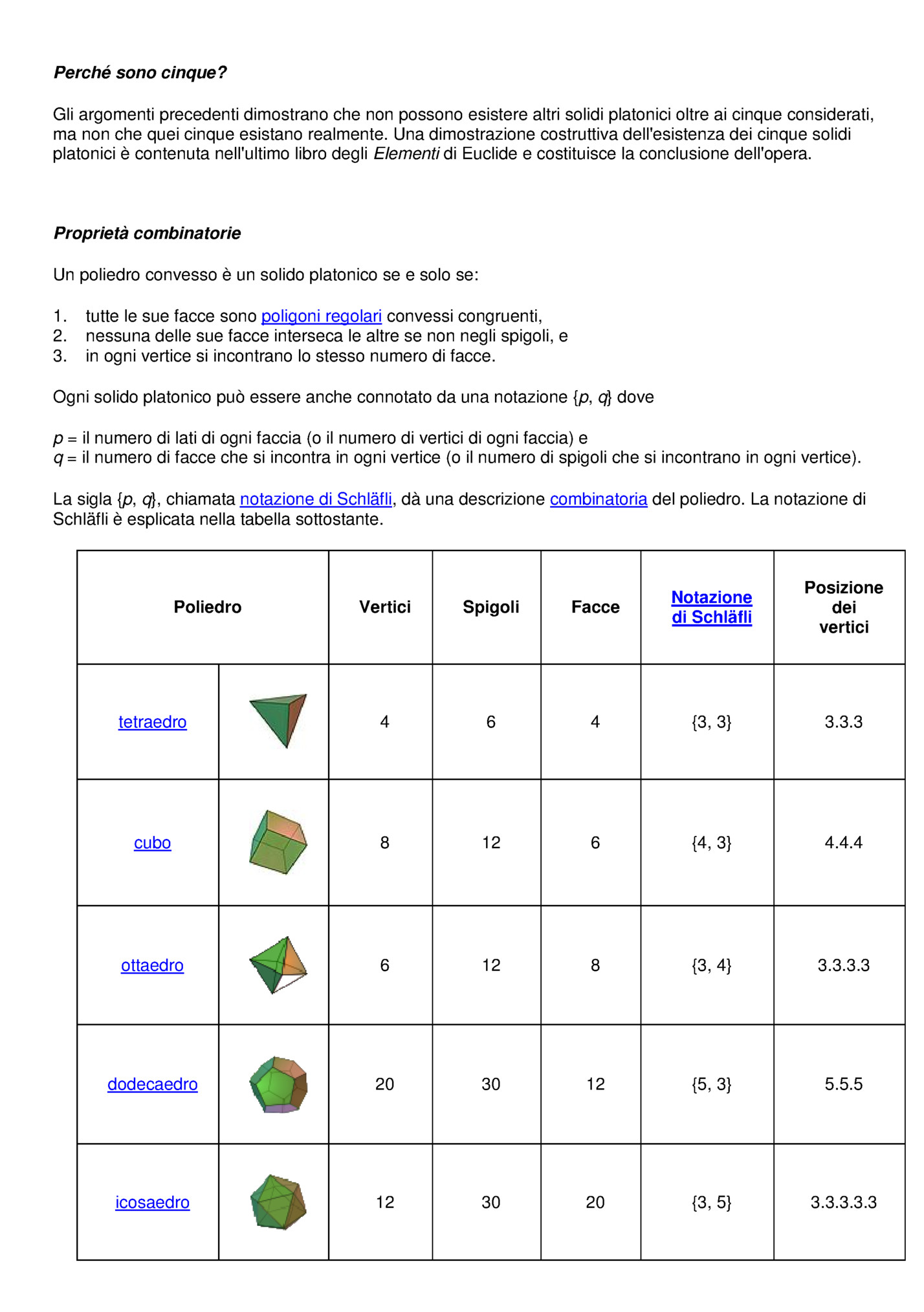
Gli argomenti precedenti dimostrano che non possono esistere altri solidi platonici oltre ai cinque considerati, ma non che quei cinque esistano realmente. Una dimostrazione costruttiva dell'esistenza dei cinque solidi platonici è contenuta nell'ultimo libro degli Elementi di Euclide e costituisce la conclusione dell'opera. Proprietà combinatorie Un poliedro convesso è un solido platonico se e solo se: 1. 2. 3. tutte le sue facce sono poligoni regolari convessi congruenti, nessuna delle sue facce interseca le altre se non negli spigoli, e in ogni vertice si incontrano lo stesso numero di facce. Ogni solido platonico può essere anche connotato da una notazione {p, q} dove p = il numero di lati di ogni faccia (o il numero di vertici di ogni faccia) e q = il numero di facce che si incontra in ogni vertice (o il numero di spigoli che si incontrano in ogni vertice). La sigla {p, q}, chiamata notazione di Schläfli, dà una descrizione combinatoria del poliedro. La notazione di Schläfli è esplicata nella tabella sottostante. Vertici Spigoli Facce Notazione di Schläfli Posizione dei vertici tetraedro 4 6 4 {3, 3} 3.3.3 cubo 8 12 6 {4, 3} 4.4.4 ottaedro 6 12 8 {3, 4} 3.3.3.3 dodecaedro 20 30 12 {5, 3} 5.5.5 icosaedro 12 30 20 {3, 5} 3.3.3.3.3 Poliedro
La dualità poliedrale, cioè la trasfigurazione di un poliedro in un secondo poliedro che presenta rispettivamente i vertici, gli spigoli e le facce corrispondenti alle facce, agli spigoli e al vertici del primo e che presenta le conseguenti relazioni di incidenza fra questi tre tipi di oggetti, è una involuzione che trasforma tetraedri in tetraedri e scambia cubi con ottaedri e dodecaedri con icosaedri. La elevata regolarità di solidi platonici si rispecchia nel fatto che ciascuno di essi ha associato un esteso gruppo di simmetria. Questi gruppi si possono considerare sottogruppi dei gruppi di simmetria dei vertici o dei gruppi di simmetria degli spigoli o dei gruppi di simmetria delle facce. I gruppi di simmetria di due solidi platonici duali sono isomorfi: infatti per dualità le permutazioni dei vertici di un poliedro diventano permutazioni delle facce del poliedro duale (mentre le permutazioni degli spigoli di un poliedro diventano permutazioni degli spigoli del duale). Il gruppo di simmetria del tetraedro viene indicato con Td, il gruppo di simmetria del cubo e dell'ottaedro con Oh, il gruppo di simmetria dell'icosaedro e del dodecaedro con Ih. Solidi platonici e cristalli Alcuni cristalli assumono la forma di solidi regolari: ad esempio il cloruro di sodio, il comune sale da cucina, si dispone in cristalli cubici, mentre il fluoruro di calcio, cioè la fluorite, si presenta in forma di ottaedri regolari. Sono poi molti i cristalli che si dispongono seguendo composizioni e varianti dei solidi platonici; questo equivale a dire che i rispettivi reticoli cristallini presentano spiccate proprietà di simmetria. Tali proprietà hanno un ruolo fondamentale per la loro classificazione. In altre dimensioni Può essere interessante notare che in uno spazio a quattro dimensioni esistono sei politopi regolari, mentre da cinque dimensioni in su ne esistono solamente tre (gli analoghi del cubo, del tetraedro regolare e dell'ottaedro regolare). Naturalmente nello spazio bidimensionale i poligoni regolari sono invece infiniti. Cenni storici Le regolarità dei solidi platonici sono straordinariamente suggestive: questo ha fatto sì che venissero ampiamente studiati fin dall'antichità, spesso cercando in essi significati nascosti e attribuendo a loro valori esoterici. Essi furono oggetto di studio di Pitagora e Platone. Quest'ultimo, nel Timeo, associò ad ognuno di essi un elemento: al tetraedro il fuoco, al cubo la terra, all'ottaedro l'aria, all'icosaedro l'acqua, mentre ritenne che il dodecaedro fosse la forma dell'universo. Essi furono poi studiati con ben maggiore razionalità dai geometri greco-alessandrini. Le costruzioni di questi solidi sono contenute nel Libro XIII degli Elementi di Euclide. La proposizione 13 descrive la costruzione del tetraedro regolare, la proposizione 14 è dedicata all'ottaedro regolare, la proposizione 15 al cubo, la proposizione 16 all'icosaedro regolare e la proposizione 17 al dodecaedro regolare. I poliedri platonici nella storia dell'arte Come si è accennato, l'idea di Platone che i solidi regolari facciano, per così dire, da tramite sul piano gnoseologico tra i disordinati fenomeni naturali e la perfezione del mondo iperuranio, non poteva non influenzare il pensiero degli uomini del Rinascimento intriso com’era di teorie neo-platoniche. L'interesse per i solidi platonici è vivo tra matematici ed artisti rinascimentali: ne studiano le proprietà metriche Piero della Francesca (nel trattato De corporibus regularibus), Luca Pacioli e successivamente Niccolò Tartaglia e Rafael Bombelli. Si deve ricordare come Luca Pacioli pubblichi nel 1509 il De Divina Proportione, con le celebri illustrazioni di poliedri eseguite da Leonardo. Le stesse illustrazioni vengono riprese con sorprendente maestria da Fra Giovanni da Verona (c.1457-1525) nella realizzazione delle tarsie della chiesa di Santa Maria in Organo a Verona.

Fleepit Digital © 2021